GEOMETRÍA
ANALÍTICA EN EL ESPACIO
Estudia las figuras geométricas
mediante técnicas básicas del análisis matemático y del álgebra en un
determinado sistema de coordenadas.

Cada figura representa una curva en el espacio y su intersección genera uno o más puntos.
La recta en R^3
Operando en la ecuación vectorial de la recta llegamos a la
igualdad:
(x,y,z) = (xo + tl ; yo + tm ; zo + tn)
Esta igualdad se verifica si:
X = Xo+ tl
Y = Yo + tm Ecuaciones Paramétricas de la recta
Z = Zo + tn
Despejando e igualando t en las ecuaciones paramétricas se tiene:
x - xo/l = y - yo/m = z - zo/n
Recta determinada por dos puntos:

r = r1 + t(r2 - r1) Ecuación vectorial de la recta
x = x1 + t(x2 -x1)
y = y1 + t(y2 -y1) Ecuaciones paramétricas.
z = z1 - t(z2 -z1)
Distancia de un punto a una recta.

Distancia entre dos rectas:

d = (a1xa2).(ro2-r01)/|a1xa2|
Esta igualdad se verifica si:
X = Xo+ tl
Y = Yo + tm Ecuaciones Paramétricas de la recta
Z = Zo + tn
Despejando e igualando t en las ecuaciones paramétricas se tiene:
x - xo/l = y - yo/m = z - zo/n
Recta determinada por dos puntos:

r = r1 + t(r2 - r1) Ecuación vectorial de la recta
x = x1 + t(x2 -x1)
y = y1 + t(y2 -y1) Ecuaciones paramétricas.
z = z1 - t(z2 -z1)
Distancia de un punto a una recta.

Distancia entre dos rectas:
d = (a1xa2).(ro2-r01)/|a1xa2|
Ángulo entre dos rectas:

B = arccos(a1.a2) ; a1 = vector director r1 ; a2 = vector director r2
El plano:

Ax + By + Cz + D = 0 Ec. general del plano.
Ecuación segmentaria del plano.

x/a + y/b + z/c = 1 Ec. segmentaria del plano.
Ecuación normal del plano:
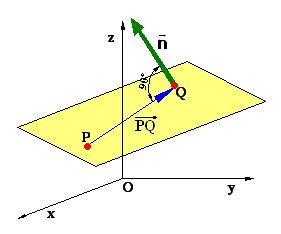
xcos(a) + ycos(b) + zcos(c) - p = 0 Ec. normal del plano
Distancia de un punto al plano:

d = Ax1 + By1 + Cz1 + D/ (A^2 + B^2 + C^2)^1/2
Ecuación del plano dado tres puntos:

(r - r1).((r2 - r1) x (r3 - r1)) = 0 Ec. vectorial del plano dado tres puntos.
Si el producto MIXTO entre tres vectores es cero, entonces los tres vectores son cooplanares.
El producto MIXTO representa geométricamente el volumen del paralelepípedo cuyas aristas son los tres vectores.
Recta determinada por dos planos:

r = (xo,yo,zo) + t(|B1XC2 - C1XB2| ; |C1A2 - A1C2| ; |A1B2 - B1A2|)
Haz de planos: n = (A1 + kA2 ; B1 + kB2 ; C1 + kC2)
Ecuación vectorial de la superficie esférica:

(x - xo)^2 + (y - yo)^2 + (z -zo)^2 = R^2
Funciones vectoriales de variable real:

F : I ------ R^n
t ------- F(t) = (f1(t), f2(t), f3(t)........., fn(t))
Derivación e Integración de funciones vectoriales:

B = arccos(a1.a2) ; a1 = vector director r1 ; a2 = vector director r2
El plano:

Ax + By + Cz + D = 0 Ec. general del plano.
Ecuación segmentaria del plano.

x/a + y/b + z/c = 1 Ec. segmentaria del plano.
Ecuación normal del plano:

xcos(a) + ycos(b) + zcos(c) - p = 0 Ec. normal del plano
Distancia de un punto al plano:

d = Ax1 + By1 + Cz1 + D/ (A^2 + B^2 + C^2)^1/2
Ecuación del plano dado tres puntos:
(r - r1).((r2 - r1) x (r3 - r1)) = 0 Ec. vectorial del plano dado tres puntos.
Si el producto MIXTO entre tres vectores es cero, entonces los tres vectores son cooplanares.
El producto MIXTO representa geométricamente el volumen del paralelepípedo cuyas aristas son los tres vectores.
Recta determinada por dos planos:

r = (xo,yo,zo) + t(|B1XC2 - C1XB2| ; |C1A2 - A1C2| ; |A1B2 - B1A2|)
Haz de planos: n = (A1 + kA2 ; B1 + kB2 ; C1 + kC2)
Ecuación vectorial de la superficie esférica:

(x - xo)^2 + (y - yo)^2 + (z -zo)^2 = R^2
Funciones vectoriales de variable real:

F : I ------ R^n
t ------- F(t) = (f1(t), f2(t), f3(t)........., fn(t))
Derivación e Integración de funciones vectoriales:

No hay comentarios:
Publicar un comentario